FÍSICA II

GASTO VOLUMETRICO

El caudal volumétrico o tasa de flujo de fluidos es el volumen de fluido que pasa por una superficie dada en un tiempo determinado. Usualmente es representado con la letra Q mayúscula.
Algunos ejemplos de medidas de caudal volumétrico son: los metros cúbicos por segundo (m3/s, en unidades básicas del Sistema Internacional) y el pie cúbico por segundo (cu ft/s en el sistema inglés de medidas).
Dada un área A, sobre la cual fluye un fluido a una velocidad uniforme v con un ángulo \theta desde la dirección perpendicular a A, la tasa del caudal volumétrico es:
Q = A \cdot v \cdot \cos \theta
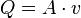
En el caso de que el caudal sea perpendicular al área A, es decir, \theta = 0, la tasa del flujo volumétrico es:                    Q = A \cdot v





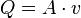
TEOREMA DE BERNOULLI


El principio de Bernoulli, también denominado ecuación de Bernoulli o Trinomio de Bernoulli, describe el comportamiento de un fluido en reposo moviéndose a lo largo de una corriente de agua. Fue expuesto por Daniel Bernoulli en su obra Hidrodinámica (1738) y expresa que en un fluido ideal (sin viscosidad ni rozamiento) en régimen de circulación por un conducto cerrado, la energía que posee el fluido permanece constante a lo largo de su recorrido. La energía de un fluido en cualquier momento consta de tres componentes:

    Cinética: es la energía debida a la velocidad que posea el fluido.Potencial gravitacional: es la energía debido a la altitud que un fluido posea.Energía de flujo: es la energía que un fluido contiene debido a la presión que posee.La siguiente ecuación conocida como “Ecuación de Bernoulli” (Trinomio de Bernoulli) consta de estos mismos términos.<br /><br /><br /><br /><br /> \frac{V^2 \rho}{2}+{P}+{\rho g z}=constante<br /><br /><br /><br /><br /> donde:
    • V = velocidad del fluido en la sección considerada.
    • \rho = densidad del fluido.
    • P = presión a lo largo de la línea de corriente.
    • g = aceleración gravitatoria
    • z = altura en la dirección de la gravedad desde una cota de referencia.
    Para aplicar la ecuación se deben realizar los siguientes supuestos:Viscosidad (fricción interna) = 0 Es decir, se considera que la línea de corriente sobre la cual se aplica se encuentra en una zona ‘no viscosa’ del fluido.Caudal constanteFlujo incompresible, donde ρ es constante.La ecuación se aplica a lo largo de una línea de corriente o en un flujo rotacionalAunque el nombre de la ecuación se debe a Bernoulli, la forma arriba expuesta fue presentada en primer lugar por Leonhard Euler.Un ejemplo de aplicación del principio lo encontramos en el flujo de agua en tubería.Cada uno de los términos de esta ecuación tiene unidades de longitud, y a la vez representan formas distintas de energía; en hidráulica es común expresar la energía en términos de longitud, y se habla de altura o cabezal, esta última traducción del inglés head. Así en la ecuación de Bernoulli los términos suelen llamarse alturas o cabezales de velocidad, de presión y cabezal hidráulico, del inglés hydraulic head; el término z se suele agrupar con P/\gamma (donde \gamma = \rho g ) para dar lugar a la llamada altura piezo métrica o también carga piezométrica.[editar]Características y consecuencia

    \overbrace{{V^2 \over 2 g}}^{\mbox{cabezal de velocidad}}+\overbrace{\underbrace{\frac{P}{\gamma}}_{\mbox{cabezal de presión}} + z}^{\mbox{altura o carga piezométrica}} = \overbrace{H}^{\mbox{Cabezal o Altura hidráulica}}

    También podemos reescribir este principio en forma de suma de presiones multiplicando toda la ecuación por \gamma, de esta forma el término relativo a la velocidad se llamará presión dinámica, los términos de presión y altura se agrupan en la presión estática.

    Esquema del efecto Venturi.

    \underbrace{\frac{\rho V^2}{2}}_{\mbox{presión dinámica}}+\overbrace{P+ \gamma z}^{\mbox{presión estática}}=constante

    o escrita de otra manera más sencilla:q+p=p_0dondeq=\frac{\rho V^2}{2}p=P+ \gamma zp_0 es una constante-Igualmente podemos escribir la misma ecuación como la suma de la energía cinética, la energía de flujo y la energía potencial gravitatoria por unidad de masa:

    \overbrace{\frac{{V}^2}{2}}^{\mbox{energía cinética}}+\underbrace{\frac{P}{\rho}}_{\mbox{energía de flujo}}+\overbrace{g z}^{\mbox{energía potencial}} = constante

    Aplicaciones del Principio de Bernoulli

    ChimeneaLas chimeneas son altas para aprovechar que la velocidad del viento es más constante y elevada a mayores alturas. Cuanto más rápidamente sopla el viento sobre la boca de una chimenea, más baja es la presión y mayo

     

    TuberíaLa ecuación de Bernoulli y la ecuación de continuidad también nos dicen que si reducimos el área transversal de una tubería para que aumente la velocidad del fluido que pasa por ella, se reducirá la presión.  es la diferencia de presión entre la base y la boca de la chimenea, en consecuencia, los gases de combustión se extraen mejor.
    Natación
    La aplicación dentro de este deporte se ve reflejado directamente cuando las manos del nadador cortan el agua generando una menor presión y mayor propulsión.
    En un carburador de automóvil, la presión del aire que pasa a través del cuerpo del carburador, disminuye cuando pasa por un estrangulamiento. Al disminuir la presión, la gasolina fluye, se vaporiza y se mezcla con la corriente de aire.
    La tasa de flujo está dada por la ecuación de Bernoulli. 
    En oxigeno terapia  la mayor parte de sistemas de suministro de débito alto utilizan dispositivos de tipo Venturi, el cual esta basado en el principio de Bernoulli.

    TEOREMA DE TORRICELLI

    serbatoio
    Es una aplicación que dio origen del principio de Bernoulli y estudia el flujo de un líquido contenido en un recipiente, a través de un pequeño orificio, bajo la acción de la gravedad. A partir del teorema de Torricelli se puede calcular el caudal de salida de un líquido por un orificio. “La velocidad de un líquido en una vasija abierta, por un orificio, es la que tendría un cuerpo cualquiera, cayendo libremente en el vacío desde el nivel del líquido hasta el centro de gravedad del orificio”.
    El experimento que realizo fue el siguiente: Cogió un tubo de un metro de largo y lo llenó hasta el borde con mercurio. A continuación tapó con el dedo el extremo abierto, dio la vuelta al tubo e introdujo su extremo, sin que se derramara nada, en un recipiente que también contenía mercurio. Quitó el dedo y observó que el mercurio descendía en el interior del tubo hasta alcanzar una altura de 76 cm en lugar del metro inicial.
    Sobre el punto B actúa la presión atmosférica y sobre el punto A sólo actúa la presión hidrostática de la columna de mercurio. Como ambos puntos están en la misma horizontal de un mismo líquido deben estar sometidos a la misma presión, basta calcular la presión del mercurio en A para obtener la presión atmosférica en B.
    pB = patm = pA= dHg · g · h = 13600 · 9,8 · 0,76 = 101300 Pa
    Este valor de 101300 Pa se conoce como presión atmosférica normal a nivel del mar y define una unidad de presión bastante habitual: la “atmósfera” que equivale a esos Pascales. También es frecuente utilizar como unidad de presión “los milímetros de mercurio” (mmHg), 760 mmHg equivalen a una atmósfera de presión.
    1 atm = 760 mmHg = 101300 Pa
    La presión atmosférica varía con la altitud, a mayor altitud menos aire encima y por tanto menos presión, también influye la situación meteorológica de tal manera que cuando está cubierto la presión baja y si está despejado sube, por eso la medida de la presión atmosférica es muy útil en meteorología. Los instrumentos para medir la presión atmosférica se llaman barómetros, hoy en día el barómetro de mercurio no se utiliza, se utilizan los barómetros aneroides más prácticos, en éstos la presión suele medirse en milibares (mbar), la equivalencia es de 1013 mbar = 1 atmósfera.
    A partir del teorema de Torricelli se puede calcular el caudal de salida de un líquido por un orificio. La velocidad de un líquido en una vasija abierta, por un orificio, es la que tendría un cuerpo cualquiera, cayendo libremente en el vacío desde el nivel del líquido hasta el centro de gravedad del orificio.
    SF
    Donde:

    • Vt= la velocidad teórica del líquido a la salida del orificio.
    • V0= la velocidad de aproximación o inicial.
    • h= la distancia desde la superficie del líquido al centro del orificio.
    • g= la aceleración de la gravedad.
    • Vt= la velocidad real media del líquido a la salida del orificio
    • Cu= el coeficiente de velocidad.

    Para velocidades de aproximación bajas, la mayoría de los casos, la expresión anterior se transforma en:
    dfd
    Donde:

    • Vt= la velocidad real media del líquido a la salida del orificio
    • Cu= el coeficiente de velocidad.

    TEMPERATURA Y ESCALAS TERMOMETRICAS


    La Temperatura

    Es una magnitud física escalar que nos indica el grado de agitación de las moléculas de un cuerpo. Es decir, cuanto mayor sea el movimiento de las moléculas de un cuerpo, mayor será su temperatura.
    La unidad de temperatura en el SI es el Kelvin(K).

    Termómetro

    El termómetro es un instrumento empleado para medir la temperatura de un cuerpo. Hay muchos tipos de termómetros.Los más utilizados contienen un líquido en su interior que puede ser mercurio o alcohol coloreado. Este tipo de termómetros funciona gracias  a una propiedad de los líquidos  de dilatarse al aumentar la temperatura y de contraerse  cuando disminuye su temperatura. Los termómetros contienen un pequeño depósito con el líquido, conectado a un tubo muy fino(capilar), por el que se puede elevar la sustancia, cuando aumenta la temperatura, el líquido se dilata y sube por el interior del tubo.
    Todos los termómetros tienen una escala de medición que ha sido previamente establecida.
    La temperatura corporal normal de los seres humanos varía entre 36,5 °C y 37,5 °C.
    Hipotermia.-Cuando la temperatura corporal es inferior a los 36 °C
    Febrícula .-cuando la temperatura es de 37,1°C  a 37,9 °C
    Hipertermia  o fiebre.-cuando la temperatura es igual o superior a 38 °C.
    TERMOMETROS

    Escalas Termométricas

    1.-Escala Celsius

    En esta escala se asigna el cero (0°C) a la temperatura en la que el agua se congela y el número cien (100°C), a la temperatura  en la que el agua hierve o vaporiza. El intervalo entre el punto de congelación y el de ebullición del agua se divide en 100 partes iguales y a cada uno se le denomina un grado Celsius.(1°C).Es la escala más utilizada.

    2.-Escala Fahrenheit

    En esta escala se asigna el número treinta y dos (32 °F)  a la temperatura en la que el agua se congela o solidifica, y el número doscientos doce(212°F) a la temperatura en la que el agua hierve o vaporiza. Esta escala es de uso común en Estados Unidos e Inglaterra.

    3.-Escala Kelvin

    En esta escala se asigna el cero (0°K) a la temperatura más baja posible, también denominada “cero absoluto”, que corresponde en la escala Celsius a -273 y al punto de congelamiento del agua corresponde a 273 K. Es la escala empleada en las investigaciones científicas.

    Conversión de escalas termométricas

    1.- De Celsius a Fahrenheit o viceversa     2.-De  Celsius a Kelvin y viceversa
    C   =   F – 32                                                                                                 K  =  C   + 273
    5             9
    EJEMPLO
    1.-Un día de verano en una determinada ciudad, la temperatura llegó a medir 35 °C. Expresa esta temperatura en Fahrenheit y Kelvin.
    C    =   F – 32               Rpta: F   = 95                                        Luego a Kelvin
    5            9                                                                                        K  =  C   + 273
    35    =  F – 32                                                                                 K  = 35  + 273
    5               9                                                                                     K  = 308

    DILATACIÓN

    Los efectos más comunes que causan las variaciones de temperatura en cuerpos o sustancias, son los cambios de sus dimensiones y de fase.
    Cuando un cuerpo o sustancia, sufre un cambio en sus dimensiones, pero no de fase debido a la temperatura; se trata de un proceso de dilatación.

    CAUSA DE LA DILATACIÓN

    En un sólido las moléculas tienen una posición razonablemente fija dentro de él. Cada átomo de la red critalina vibra sometido a una fuerza asociada a un pozo de potencial, la amplitud del movimiento dentro de dicho pozo dependerá de la energía total de átomo o molécula. Al absorber calor, la energía cinética promedio de las moléculas aumenta y con ella la amplitud media del movimiento vibracional ya que la energía total será mayor tras la absorción de calor. El efecto combinado de este incremento es lo que da el aumento de volumen del cuerpo.
    En los gases el fenómeno es diferente, ya que la absorción de calor aumenta la energía cinética media de las moléculas lo cual hace que la presión sobre las paredes del recipiente aumente. El volumen final por tanto dependerá en mucha mayor medida del comportamiento de las paredes.Según su naturaleza cada cuerpo posee lo que se llama coeficiente de dilatación térmica, cuyo símbolo es “alfa” y su unidad de medida es 1/°C o °C-1, algunos valores son:


                                                     




     SUSTANCIAVALOR SUSTANCIA VALOR 
     PLOMO 
    29*10^-6
    		 ALUMINIO 
    29*10^-6
     HIELO 
    52*10^-6
    		 BRONCE 
    29*10^-6
     CUARZO 
    0,6*10^-6
    		 COBRE 
    29*10^-6
     HULE DURO 
    80*10^-6
    		 HIERRO 
    29*10^-6
     ACERO 
    12*10^-6
    		 LATON 
    29*10^-6
     MERCURIO 
    182*10^-6
    		 VIDRIO (NORMAL) 
    29*10^-6
     ORO 
    14*10^-6
    		 VIDRIO(PIREX) 
    29*10^-6

    Existen tres tipos de dilatación; a continuación los mencionaremos:


    Ø  Dilatación lineal
    Esto se lleva a cabo en materiales, como son los alambres, varillas o barras, al calentarse aumentan su longitud, y por tanto su volumen

    La parte en color negro de la figura corresponde al incremento de volumen lineal de la dilatación.
    A esta propiedad se le denomina dilatación lineal, y se representa con la letra “alfa”, se define como el incremento de longitud que experimenta una varilla de cualquier longitud y material determinado  al elevarse la temperatura.
    Podemos usar la siguiente fórmula para determinar la dilatación lineal:

    "alfa"= Lf-Lo/Lo (Tf-To)


    Ø  Dilatación de superficie
    Este caso se presenta en cuerpos de dos dimensiones como son las placas, ocurre cuando se expanda lo ancho y largo debido al calor. Podemos calcular la dilatación superficial con la siguiente fórmula:

                                                                      r=2[Lf-Lo/Lo (Tf-To)]




    Ø      Dilatación volumétrica
     
    Esto se refiere al aumento del tamaño de los cuerpos en sus tres dimenciones por efecto de la dilatacion, y podemos conoces este valor con la siguiente formula: 
                                                                      B=3[Lf-Lo/Lo(Tf-To)]
     



    Tambien es posible conocer el aumento del volumen en un proceso de dilatacion, y lo hacemos con la siguiente formula:
    Vf=Vo[1-B(Tf-To)]



    Los simbolos que hemos utilizado en las formulas anteriores se explican a continuacion:

    • "alfa"= Coeficiente de dilatacion lineal
    • r= Coeficiente de dilatacion superficial
    • B= Coeficiente de dilatacion cubica
    • Lf= Longitud final
    • Lo= Longitud inicial
    • Tf= Temperatura final
    • To= Temperatira inicial
    • Vf= Volumen final
    • Vo= volumen inicial


    Comentarios

    Publicar un comentario

    Entradas populares de este blog

    Imagen
    FISICA II CALOR Y CANTIDAD DE CALOR CALOR.-   Se llama calor a la propagacion o flujo de la energía entre cuerpos que se ponen en contacto, es decir, el calor es la energía en movimiento. Todos los cuerpos de la naturaleza tienden a un estado final llamado equilibrio termodinámico con el medio que los rodea o con otros cuerpos en contacto, es decir adquieren la misma temperatura. Capacidad Calorifica (C).-  Se define como la cantidad de calor que se debe suministrar o sustraer a un cuerpo o sustancia para elevar o disminuir su temperatura en un grado centigrado, es decir. Siendo T0, T las temperaturas inicial y final respectivamente. La capacidad calorifica es una cantidad física escalar que depende de la composicion y estructura interna del cuerpo o sustancia, lo cual implica que cada cuerpo o sustancia tiene su propia capacidad calorifica. Calor específico (Ce).-   Se define como la cantidad de calor (Q), que se debe suministrar a la masa "m" de un cyu...
    Leer más
    Imagen
                                   FISICA II               ESTADOS DE AGREGACIÒN En fìsica  y quìmica  se observa que, para cualquier sustancia  o mezcla, modificando sus condiciones de temperatura  o presiòn , pueden obtenerse distintos estados o fases, denominados estados de agregación de la materia, en relación con las fuerzas de uniòn  de las partículas (moléculas, átomos o iones) que la constituyen. Todos los estados de agregación poseen propiedades y características diferentes; los más conocidos y observables cotidianamente  son cuatro, llamados fases sòlida , lìquida , gaseosa  y plasmàtica .                                                    Estado Sòlido: Los objetos en estado sólid...
    Leer más